中学受験の算数で初めて習う特殊算が「つるかめ算」と「弁償算」、という方も多いでしょう。
しかし、中には
- 「つるかめ算って結局何なの?」
- 「つるかめ算と弁償算って何が違うの?」
といった疑問をお持ちの方もいらっしゃるのではないでしょうか。
ただ、これらの疑問に答えられる受験生は意外と多くないんです…!
そして、これらがわかっていないと入試問題どころか、5年生後期でつまづく可能性が非常に高いです…!
そこで本記事は
- つるかめ算と弁償算はいつ使うのか
- つるかめ算と弁償算は何が違うのか
- つるかめ算と弁償算の解き方
を解説していきます!
つるかめ算・弁償算 | いつ使うのか

結論から言うと、つるかめ算と弁償算は
2種類の合計がわかっていて、それぞれの配分を知りたい時
に使います
例題を用いて詳しく説明しましょう。
つるかめ算の例題
例えば、このようなつるかめ算の典型的な問題が出たとしましょう。
50円切手と80円切手が合わせて35枚あり、合計の金額は1900円です。50円切手は何枚ありますか。
この場合、問題文の条件は
- 切手の枚数の合計:35枚
- 切手の金額の合計:1900円
- 求めるもの:50円切手を何枚買ったか (≒切手をそれぞれ何枚ずつ買ったか)
となります。
「枚数の合計」と「金額の合計」という2種類の合計から、「切手の種類ごとの枚数の配分」を求める問題であることから、この問題ではつるかめ算を使うと判断できるわけです。
弁償算の例題
以下のような典型的な弁償算の問題が出たときを、同様に考えてみましょう。
A君はガラスのコップを100個運びます。1個運ぶごとに報酬として10円もらいます。しかし、コップを割ってしまうと1個につき70円弁償します。A君はコップを運び終え、760円もらいました。全部で何個のコップを割ったでしょうか。
この場合、問題文の条件は
運ぶコップの数の合計:100個
貰ったお金の合計:760円
求めるもの:壊したコップの数 (≒運んだコップと壊したコップのそれぞれの数)
となります。
「コップの数の合計」と「お金の合計」という2種類の合計から、「運んだコップと壊したコップの配分」を求める問題であることから、この問題は弁償算を使うと判断できるわけです。
つるかめ算と弁償算は2種類の合計がわかっていて、それぞれの配分を知りたい時に使う。
これがわかっているだけで、テストの点数はかなり安定します。
なぜなら、「なぜその知識を使うのか」を理解できているからです。
こちらの記事で詳しく解説していますので、併せてご覧ください。
つるかめ算・弁償算 | 違い

ここまでで、つるかめ算と弁償算はどのような時に使うのかをお話しましたが、この2つの特殊算はどのように使い分けるのでしょうか。
結論から言うと、
- 弁償算:マイナスが発生するとき
- つるかめ算:それ以外
です。
マイナスが発生する条件があるのは弁償算で、マイナスが発生しなければつるかめ算
ということになります。
先ほどと同様、例題で説明しましょう。
弁償算の例題
まずは弁償算から説明します。先ほどの例題と同じもので考えましょう。
A君はガラスのコップを100個運びます。1個運ぶごとに報酬として10円もらいます。しかし、コップを割ってしまうと1個につき70円弁償します。A君はコップを運び終え、760円もらいました。全部で何個のコップを割ったでしょうか。
この場合、問題文の条件は
- 運ぶコップの数の合計:100個
- 貰ったお金の合計:760円
- 求めるもの:壊したコップの数 (≒運んだコップと壊したコップのそれぞれの数)
ですので、「使う計算はつるかめ算or弁償算だ」と判断できるわけですが
ポイントは問題文中の「コップを割ってしまうと1個につき70円弁償します」という部分です。
弁償するということはつまり、マイナスが発生しているわけで、この「マイナスの発生」という要素がつるかめ算にはありません。
つるかめ算の例題
同様に先ほどのつるかめ算の例題を見てみましょう。
50円切手と80円切手が合わせて35枚あり、合計の金額は1900円です。50円切手は何枚ありますか。
こちらも問題の条件は
- 切手の枚数の合計:35枚
- 切手の金額の合計:1900円
- 求めるもの:50円切手を何枚買ったか (≒切手をそれぞれ何枚ずつ買ったか)
ですので、「使う計算はつるかめ算or弁償算だ」と判断できるわけですが
先ほどの弁償算の例題とは異なり、この問題にはマイナスの発生要素がありません。
それゆえ、「使うのはつるかめ算」と判断できます。
- つるかめ算と弁償算は2種類の合計がわかっていて、それぞれの配分を知りたい時に使う。
- マイナスが発生する条件があるのは弁償算で、マイナスが発生しなければつるかめ算
つるかめ算・弁償算 | 解き方

ここまでで、「つるかめ算と弁償算をいつ使うのか」・「何が違うのか」を解説しました。
ただ、実はこの2種類の特殊算はそれぞれ使える解法が若干異なります。
結論から言いますと、それぞれで使える解法は
- つるかめ算:面積図 or 表で整理
- 弁償算:表で整理
となります。
こちらも例題で解説しましょう。
つるかめ算を面積図で解く
先ほどのつるかめ算の例題を用いて考えます。
50円切手と80円切手が合わせて35枚あり、合計の金額は1900円です。50円切手は何枚ありますか。
こちらの条件を面積図に整理すると以下の通りになります。
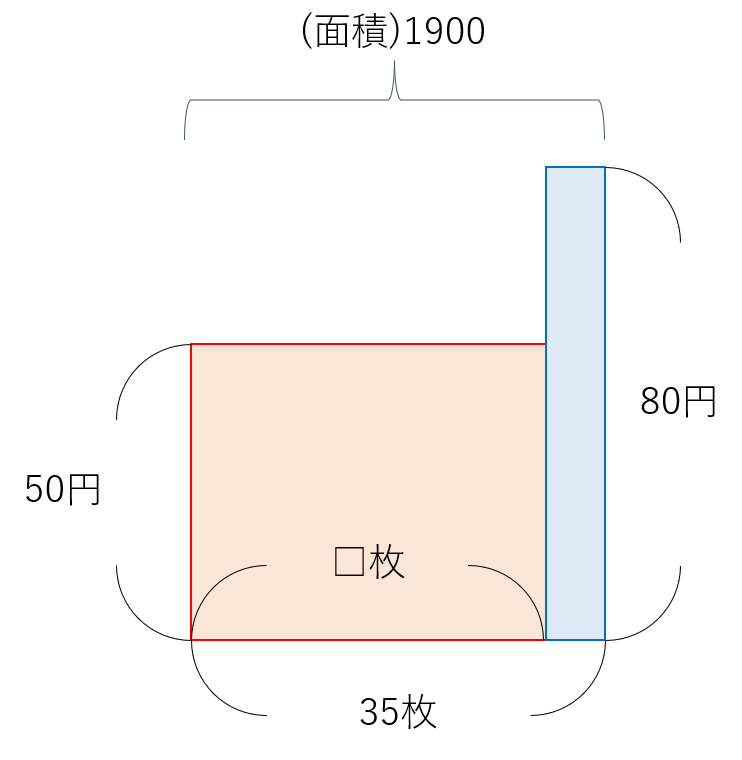
赤い部分の面積が50円切手の値段の合計、青い部分の面積が80円切手の値段の合計です。
つまり、赤い部分の面積+青い部分の面積=1900 となります。
この時、80×35-1900を計算すると以下の図のグレー部分の面積となります。
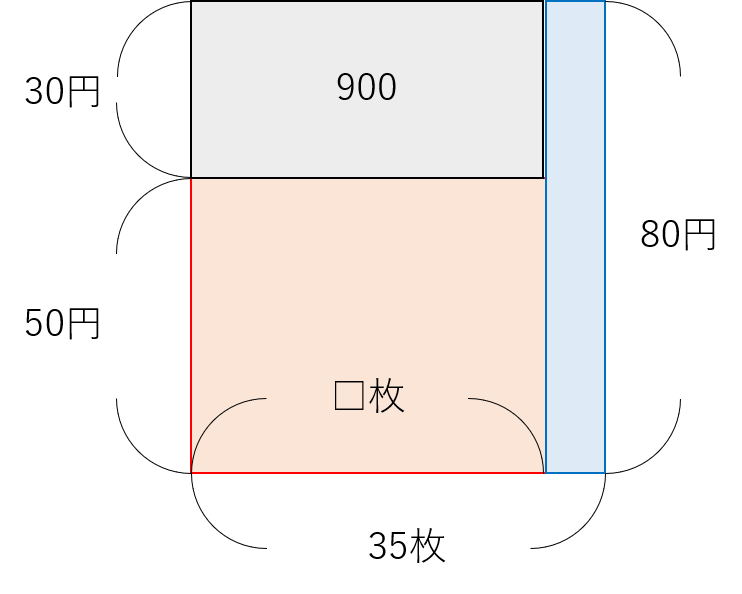
求めたい数は図中の□なので、式は
(80×35-1900)÷ 30 = 30
よって、50円切手は30枚購入したことがわかります。
これが面積図の解き方です。
つるかめ算を表で解く
次に、つるかめ算を表で解く考え方です。
表を使って解くうえで重要なのは「もし全部〇〇だったら」という考え方をする点です。
さきほどの例題で「もし購入した35枚すべてが50円切手だった場合」を表にまとめる場合、以下のように整理できます。

ここから、「もし50円切手を34枚、80円切手を1枚買ったら」「もし50円切手を34枚、80円切手を2枚買ったら」、と1枚ずつ80円切手の枚数を増やしていくと、以下の表のように合計金額は30円ずつ増加していきます。
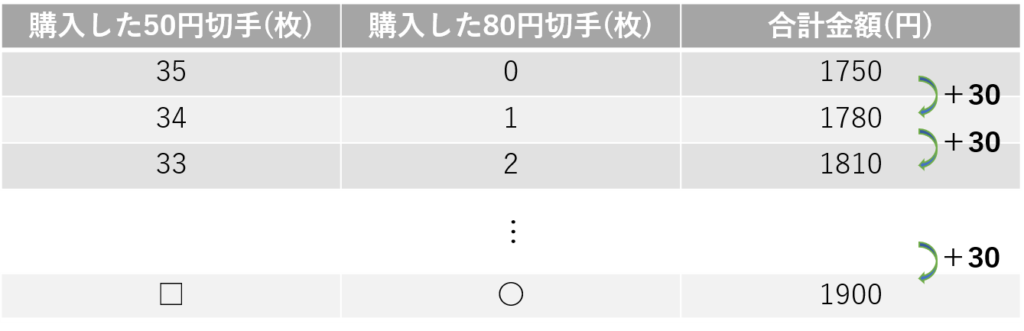
求めたいのは合計金額が1900円の時なので
(1900-1750)÷30=5 より、80円切手を5枚買ったことがわかります。(表中の〇)
ゆえに、購入した50円切手の枚数は35-5=30で30枚だとわかります。(表中の□)
これが表を使った解法です。
以上のように、つるかめ算は面積図・表 どちらを使っても解くことができます。
弁償算を表で解く
次に、弁償算を表を使って解方法を考えます。
先ほどの弁償算の例題を使って考えましょう。
「A君はガラスのコップを100個運びます。1個運ぶごとに報酬として10円もらいます。しかし、コップを割ってしまうと1個につき70円弁償します。A君はコップを運び終え、760円もらいました。全部で何個のコップを割ったでしょうか。」
こちらも、つるかめ算の表の解き方同様、「もしコップを100個すべて割らずに運んだら」という考え方をします。
すると以下のように整理できます。

ここから、「もしコップを99個運び、1個割ったら」「もしコップを98個運び、2個割ったら」、と1つずつ割ったコップの数を増やしていきます。
すると、割ったコップが1つ増えるごとにもらえる金額は80円ずつ減っていくことに気付くはずです。
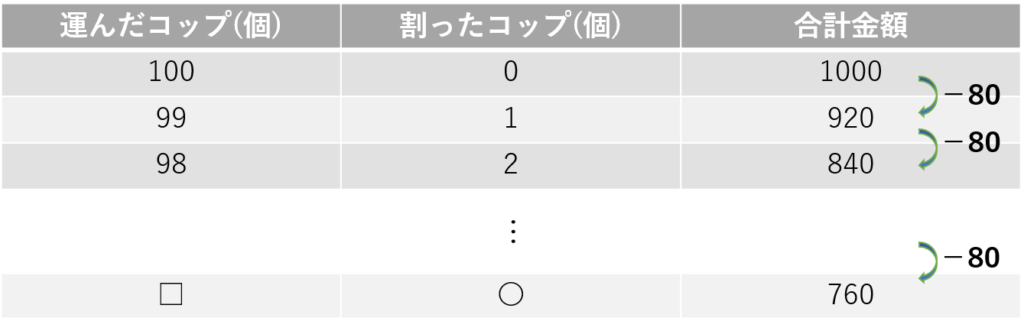
求めたいのは合計金額が760円の時なので、
(1000-760)÷80=3より、割ったコップの数が3個であることがわかります。(図中の〇)
ゆえに、答えは3です。
以上が表を使った弁償算の解法でした。
(番外編)弁償算は面積図では解けない?
ここで
- つるかめ算は表と面積図の2つの解法があるのに、弁償算は表の解法しかないのか。
- 面積図で弁償算は解けないのか
と考える方もいらっしゃるでしょうが、
弁償算は面積図では解けません
というのも、前述のとおり弁償算は「マイナスが発生する」のが特徴ですが、このマイナスを面積図で表現することができないのです。
(※厳密に言うと、表現できなくはないのですが、小学生には難しすぎます)
ゆえに、弁償算は表でしか解けない、と覚えてしまってかまいません。
まとめ
さて、本記事ではつるかめ算と弁償算について解説してきました。
ポイントは以下の通りです。
つるかめ算と弁償算は、2種類の合計がわかっていて、それぞれの配分を知りたい時に使う
- 弁償算:マイナスが発生するとき
- つるかめ算:それ以外
- つるかめ算:面積図 or 表で整理
- 弁償算:表で整理
つるかめ算と弁償算は定番の特殊算ですが、いざテストで問われるとわからなくなってしまう子が多い単元です。
また、6年生になると問題を解く過程でつるかめ算を使う場合すらあります。
逆にこの3点を覚えておけば、どんな問題にも対応できるはずです!
これを機に覚えてしまいましょう!
今回は以上です!
ありがとうございました!
皆さんの中学受験がステキな経験になりますように。




