中学受験で避けては通れない特殊算のひとつが「和差算」です。
ほとんどの中学受験生が4年生で習う超定番の単元ですが、
- 和差算って結局いつつかうの?
- 和差算の決まった解き方ってあるの?
といった疑問をお持ちの方もいらっしゃるのではないでしょうか。
これらの質問にパっと答えられる受験生は意外と多くありません…!
しかし、これがきちんと理解できていないと
比が登場する5年生後半でつまずく可能性が高いです…!
そこで本記事では
- 和差算はいつ使うのか
- 和差算の解き方
を解説します!
和差算 | いつ使うか

結論から言うと、和差算は
いくつかの数の「和」と「差」がわかっていて、それぞれの数を求めたい時
に使います。
例題を用いて詳しく説明しましょう。
例題
例えば、このような和差算の典型的な問題が出たとしましょう。
りんごとみかんが全部で25個あります。りんごの方がみかんより3個多いです。りんごとみかんはそれぞれいくつありますか?
この場合、問題文の条件は
- リンゴとミカンの個数の合計(和):25個
- リンゴとミカンの個数の差:3個
- もとめる数:リンゴとミカンそれぞれの個数
となります。
「個数の合計」と「個数の差」から「それぞれの個数」を求める問題であることから、この問題は和差算の問題だと判断できるわけです。
和差算 | 解き方

ここまでは和差算だと判断する条件を説明しましたが、次に和差算の解法について解説します。
結論から言うと
和差算は「線分図」で整理し、長さをそろえて解きます。
こちらも例題を使って説明しましょう。
例題
先ほどの例題で考えてみましょう。
りんごとみかんが全部で25個あります。りんごの方がみかんより3個多いです。りんごとみかんはそれぞれいくつありますか?
まず、文章題の条件を線分図に整理していきます。
線分図を使い整理すると以下の通りです。
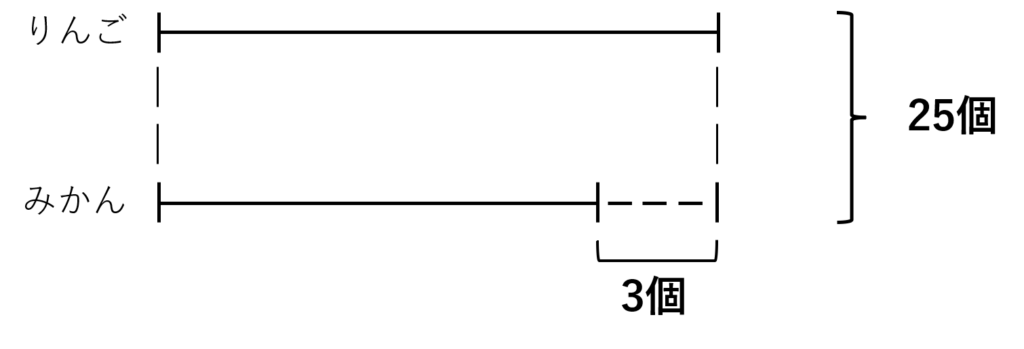
このままでは解くことはできないので、次に線分図の長さをそろえましょう。
具体的には「もしみかんがりんごと同じ個数だったら」を考えていきます。
この問題の場合、もしあとみかんが3つあればりんごと同じ数になり、その時のりんごとみかんの個数の合計は
25+3=28個になります。
これらを線分図に表すと以下の通りです。

りんごの線分図とみかんの線分図の長さがそろいました。
このとき、りんごを□個とすると、線分図より
□+□=28個であることがわかるため
りんご□個=28個÷2=14個とわかります。
みかんはりんごより3個少ないため
14-3=11個です。
以上が和差算の解き方です。
どのような和差算の問題も線分図に整理して、長さをそろえることで解くことができます。
もしそれでも解けない場合は、線分図に整理しきれていない数字があるはずです。
というもの、中学受験では使わない情報が問題文や計算式に登場することはまずありません。ですので、「線分図に整理して長さをそろえても解けない」という場合は、問題文中の見落としている情報や線分図に記入できていない数字がないか確認してみましょう。
【番外編】応用例題の解説

先ほど、和差算を使うのは
いくつかの数の「和」と「差」がわかっていて、それぞれの数を求めたい時
と解説しましたが、問題によっては文章中に「和」や「差」といった単語がなく
情報を線分図に整理する中で「和と差がわかっているから和差算だ」と気づく必要がある問題もあります。
以下の応用問題で考えてみましょう。
わさお君とお父さんの年令の和は57才で、わさお君とお母さんの年令の和は54才です。お父さんとお母さんの年令の和が85才のとき、わさお君は何才ですか?
この問題の場合、問題文の中には「和」という言葉しかないため、この時点で「和差算」と気づくことは少し難しいでしょう。ですので、いったん情報を図や表で整理する必要があります。
仮にこの文章題を線分図に整理する場合、以下の通りになります。
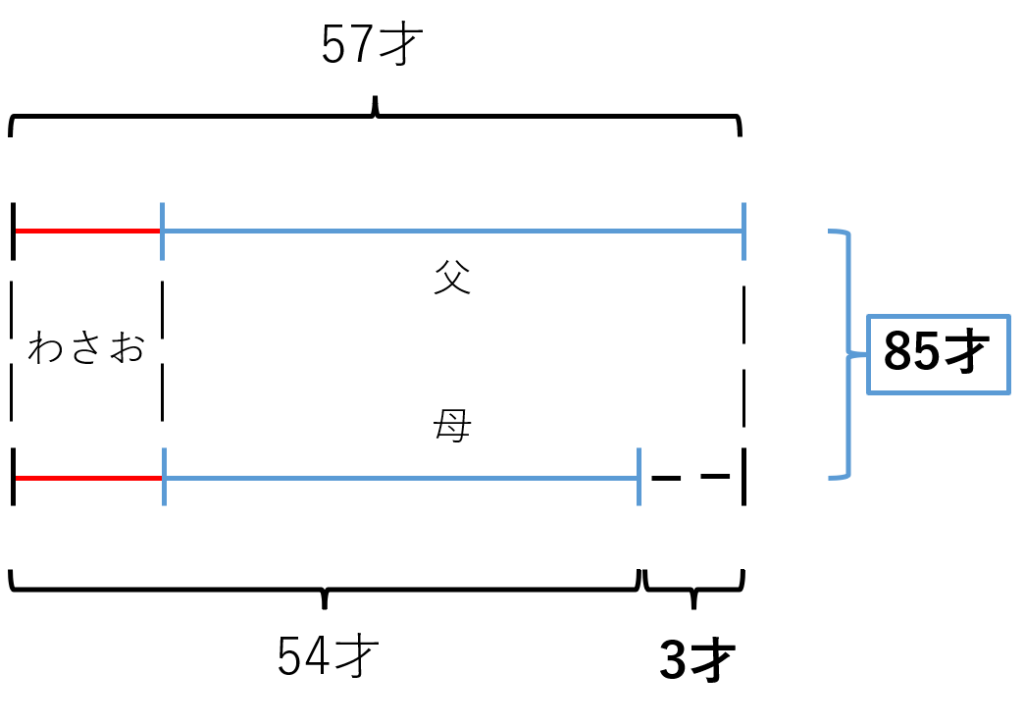
※余談ですが、複数個の線分図で同じ数値が登場する場合は左側に寄せて書きましょう。
線分図に整理すると、父と母の年齢の和は54才(文章より)で、年齢の差は
57-54=3才であることがわかります。
ここで、父の年齢と母の年齢に関しては、年齢の和と年齢の差が分かるため、父と母それぞれの年齢を和差算を使って求められることに気付くはずです。
父の年齢と母の年齢のみに絞って線分図で整理すると以下のようになります。
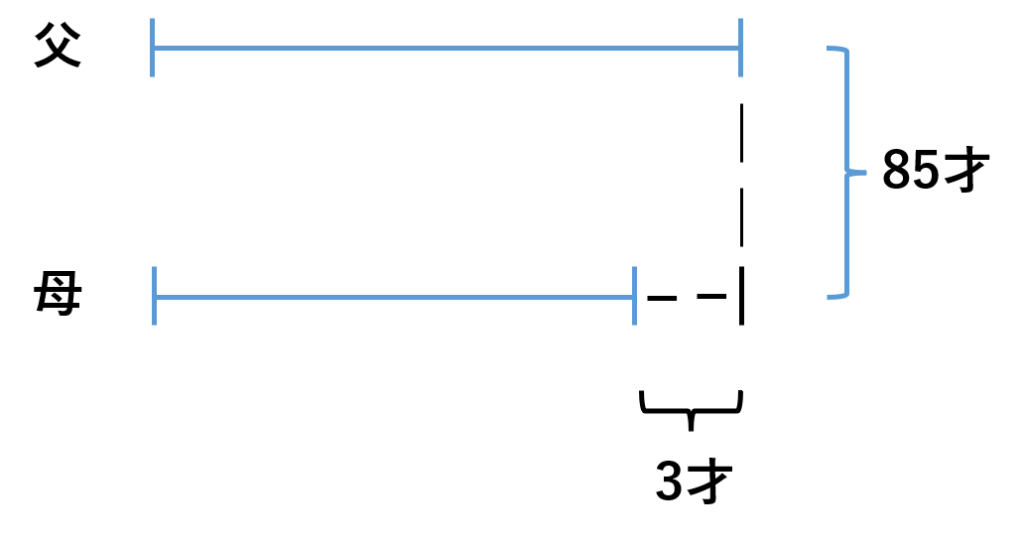
ここからは、先ほど解説した通り、線分図の長さをそろえて計算すれば父・母それぞれの年齢が求められます。
(85+3)÷2=44才…父の年齢
44-3=41才…母の年齢
よって、わさお君の年齢は
57-44=13才
となります。
※54-41=13才でも求められます
今回ご紹介した問題以外にも、文中に「和」や「差」といった単語が直接書かれていなくても和差算を使わないと解けない問題は多くあります。
そういった場合、図や表に条件を整理する中で「和」と「差」が出てきたら「和差算が使える!」と気づく必要があるのです。
まとめ
本記事では、和差算に関してご紹介しました。
ポイントをまとめると以下の通りです。
いくつかの数の「和」と「差」がわかっていて、それぞれの数を求めたい時 に使う
「線分図」で整理し、長さをそろえて解く
文中に「和」や「差」といった単語が直接書かれていなくても、図や表に条件を整理する中で「和」と「差」が出てきたら「和差算が使える」と気づく必要がある
今回は以上です!
ありがとうございました!



