周期の単元に登場する「曜日を求める問題」を日歴算といいますが、この日歴算に苦戦する生徒は少なくありません。
特に
- 全部の日にちを書き出して調べようとしてしまう
- 7で割った後どうすればいいかわからない
- 7でわったあまりから曜日を求めるところでいつも間違えてしまう
というお子さんが多いのではないでしょうか?
しかし、この日歴算
あるポイントさえ押さえておけば絶対に正解できるようになります!
そこで本記事は日歴算が苦手な方に向けて、前提知識と正しい解き方・意識すべきポイントをご紹介します。
そもそも日歴算とは?
日歴算とはその名の通り、「暦(こよみ)に関する知識を使い、曜日を求める問題」のことです。標準的なカリキュラムだと5年生で登場します。
以下のような問題が定番の出題形式です。
ある年の3月14日が木曜日の時、同じ年の7月2日は何曜日ですか。
問題の最大の特徴は
- 基準となる日付と曜日が指定されている
- 指定された日付の曜日を求める
という2点です。
先ほどの例題の場合、3/14(木)を基準となる日として、7/2の曜日を求めます。
この様に、曜日を聞かれた場合はほぼ100%日歴算の問題ですので、出題された際はまず基準となる日と曜日を求めたい日付を確認しましょう。
日歴算に必要な前提知識
日歴算を解くうえでは、必要な前提知識が3つあります。
- 曜日の周期
- 1か月の日にち
- うるう年
の3つです。
この3つを知らないと、そもそも日歴算を解くことができないので、非常に重要です。
それぞれ詳しく説明しましょう。
曜日の周期
1つ目の前提知識は曜日の周期です。
具体的には、「7日たつごとに同じ曜日がやってくる」ということです。
小学校高学年の子にとってはもはや当たり前のことかもしれませんが、「曜日は7日ごとの周期を繰り返している」という感覚を持てているかが、日歴算を解くうえでのポイントになります。
1ヶ月の日数
2つ目の前提知識は1か月の日数です。日歴算を習う上で、すべての学習塾がこの知識を扱うはずですが、月によって1か月あたりの日数は異なります。
具体的には
1月・3月・5月・7月・8月・10月・12月は31日間
4月・6月・9月・11月は30日間
2月は28日間(うるう年は除く)
です。
日歴算では基準となる日から数か月先の曜日を聞かれる問題が頻出ですが、そういった問題を解く際にこの知識は必須です。
日歴算の問題を解く前に、これらの日数を正しく把握できているか確認してみましょう。
なお、1か月あたりの日数には定番の覚え方や語呂合わせがあります!
詳しくはこちら(外部サイト)をご覧ください。
うるう年
3つ目の前提知識はうるう年です。
うるう年とは、2/29日が存在する年のことで、「普段であれば2月は28日までしかないものの、4年に1回2月29日が存在する年が来る」という点を知っているかが重要になります。
なお、うるう年かを見分ける条件は以下の3つです。
うるう年の条件①:4で割り切れる年はうるう年
(例) 2020年、2024年はうるう年
うるう年の条件②:100で割り切れる年はうるう年ではない
(例) 1900年、2000年はうるう年ではない
うるう年の条件③:400で割り切れる年はうるう年
(例) 1600年、2000年はうるう年
日歴算の中には、基準となる日から数年後の日付の曜日を問われる問題があります。そういった問題を解くうえでは、うるう年の知識がないと正しい曜日が求められません。
ただし、良心的な問題であれば、問題文中にうるう年に関する記述をしてくれている場合もあるので、あまり神経質にならなくても問題はありません。
頭の片隅に入れておきましょう。
標準的な日歴算の解き方
さてここからは標準的な日歴算の解き方をご紹介します。
今回ご紹介する解き方を再現できるようになれば、試験で出題される日歴算はもはやサービス問題になるでしょう…!
標準的な日歴算の解き方は大きく分けると4段階です。
具体的には
- 表を書く
- 曜日を求めたい日が基準となる日の何日後かを求める
- 7で割る
- 表から曜日を求める
という4段階で解きます。
先ほどご紹介した以下の例題を活用しながら、1つずつ詳しく説明していきましょう。
ある年の3月14日が木曜日の時、同じ年の7月2日は何曜日ですか。
表を書く
まずは表を書きます。
この表の書き方によって、正しく解けるかの50%は決まるので慎重にいきましょう。
まず基準となる日付の曜日から1週間分の曜日を一列に書きます。
例題の場合、基準となる日は木曜日なので以下のようになります。

次に、曜日の上に1つずつ数字を記入していきます。
この時、記入方法は左から、0,1,2…6という書き方をするので要注意です。
例題の場合、以下のようになります。

ここまでが表を書く工程です。
数字は1からではなく、0からふっていくのが最大のポイントです。
ちなみに、記入した数字は最後にまた使います。
曜日を求めたい日が基準となる日の何日後かを求める
次に、曜日を求めたい日が基準となる日の何日後かを求めます。
前工程で記入した表から一度離れて、計算で求めていきます。
例題の場合、この工程で求めるのは「7/2は3/14の何日後か」です。
順番としては
- まず3月末が3/14の何日後かを求める
- 次に6月末が3月末の何日後かを求める
- 最後に7/2が6月末の何日後かを求める
- 和を求める
という順番になります。
ポイントは、一気に求めようとするのではなく
- 基準となる日が含まれている月
- 間の数か月
- 曜日を求めたい日が含まれる月
の3つに分けて考えることです。
※前提知識の「1か月あたりの日数」の知識を使います
・3月末日が3/14の何日後か
=31日-14日=17日後
・6月末日が3月末の何日後か
=4月の日数+5月の日数+6月の日数=30日+31日+30日
=91日後
・7/2が6月末日の何日後か
=2日後
という式から、
7/2は3/14の17+91+2=110日後とわかります。
以下の図で見るとわかりやすいはずです。
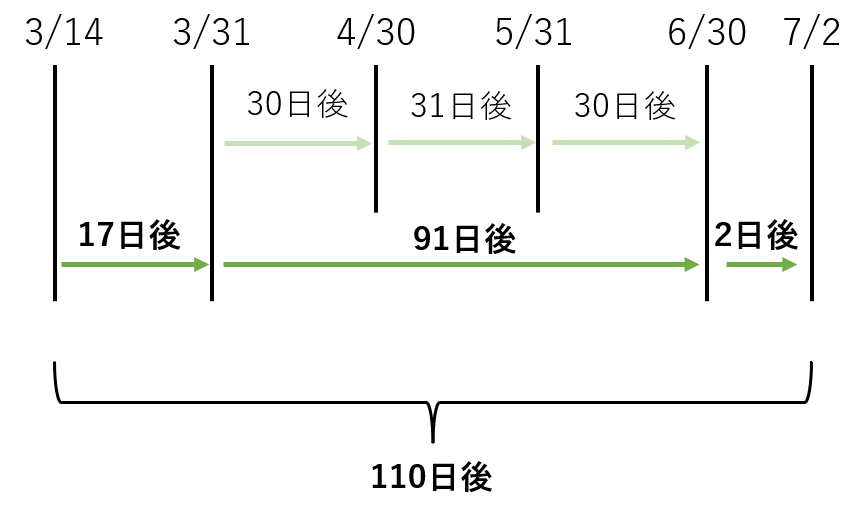
以上が2番目の工程でした。
慣れないうちは計算式だけではなく、図も書きながら整理するのがおすすめです。
なお、この過程を正しく計算できるかによって、正解にたどり着けるかがほぼ決まります。
計算は慎重にいきましょう。
7で割る
この工程では、先ほど求めた「〇日後」の数字を7で割ります。
というもの、1週間は7日間であるため、〇日後を7で割ることで、〇日後までに1週間が何回繰り返されているかを知ることができます。
さらに、7で割ったときに生じるあまりは「一週間に満たないはんぱな日数」を表しているため、この工程では「基準となる日から曜日を求めたい日までに何週間と何日あるか」を求めることになるのです。
例題の場合
7月2日は基準となる3月14日の110日後であるため
110÷7=15あまり5となります。
この時、「15あまり5」の「15」というのは「15週間」という意味です。
一方、「15あまり5」の「あまり5」は、「はんぱな5日間」という意味になります。
つまり「15あまり5」は「15週間とはんぱな5日」という意味です。
※なお、今回ご紹介している「表を使う解き方」で解けば、こうした数字の意味を理解できていなくても正解にはたどり着けます!
表から曜日を求める
最後の工程では、7で割って出た数字をもとに、表を使って曜日を求めます。
ポイントは、「7で割ったあまりと同じ数字がふられている列に日付を記入する」ということです。
例題を用いて説明しましょう。
先ほどの工程で基準となる3/14から曜日を求めたい7/2までは15週間と5日あることがわかりました。
この時、あまりとして出た「5日」に着目します。
最初に書いた表には曜日の上に数字がふられていますが、この数字とあまりとして出た「5日」が一致する列に、曜日を求めたい日付を記入します。
この例題のケースでは、5がふられている列に7月2日を記入すると、その列が火曜日の列であるため、7月2日は火曜日だとわかります。
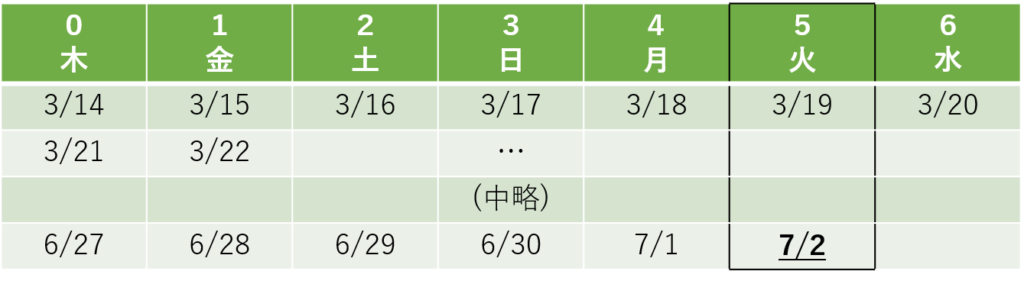
よって、この問題の答えは「火曜日」です。
以上が基本的な日歴算の解き方です。
この表を用いたやり方で解けば、7で割ったあまりの処理に迷うことがなくなります!
ぜひご活用ください!
特殊な日歴算の解き方
ここでは、特殊な日歴算の解き方を解説していきます。
特殊というのは、日付をさかのぼるタイプの日歴算のことです。
標準的な問題は解けても、日付をさかのぼるタイプの日歴算を間違えてしまう方は少なくありません…
しかし、解き方は標準的な日歴算も特殊な日歴算も解き方の大枠は同じです。
こちらもおなじく
- 表を書く
- 曜日を求めたい日が基準となる日の何日前かを求める
- 7で割る
- 表から曜日を求める
という4段階で解きます。
異なるのは
- 表の曜日と日付の書き方
- 何日後ではなく、何日前かを求める
の2つのみです。
こちらの例題を用いて解説して、詳しく解説していきます。
ある年の7月20日が日曜日の時、同じ年の4月1日は何曜日ですか。
表を書く
最初にやることとしては、標準的な問題同様、表を書きます。
まず基準となる日付の曜日から1週間分の曜日を一列に書くのですが、この時、曜日をさかのぼって書いていきます。
例題の場合、基準となる日は日曜日なので以下のようになります。

次に、曜日の上に1つずつ数字を記入していきます。
記入方法は同じく、左から0,1,2…6という具合です。
1ではなく0から書き始める点に注意しましょう。 またこの時、曜日をさかのぼって記入しているため、表の中に日付を書いていく際は日付もさかのぼって書きます。

以上が最初の工程です。
「曜日と日付をさかのぼって記入する」という点が最も重要ですので、覚えてしまいましょう!
曜日を求めたい日が基準となる日の何日前かを求める
次に曜日を求めたい日が基準となる日の何日前かを調べていきます。
この時も
- 基準となる日が含まれている月
- 間の数か月
- 曜日を求めたい日が含まれる月
の3つに分けて考えることが重要です。
例題の場合
・7/1は7/20の何日前か
=20-1=19日前
・5月初日は7/1の何日前か
=5月の日数+6月の日数=31日+30日=61日前
・4/1は5月初日の何日前か
=4月の日数=30日前
という式から、
4/1は7/20の19+61+30=110日前とわかります。
図で表すと以下の通りです。
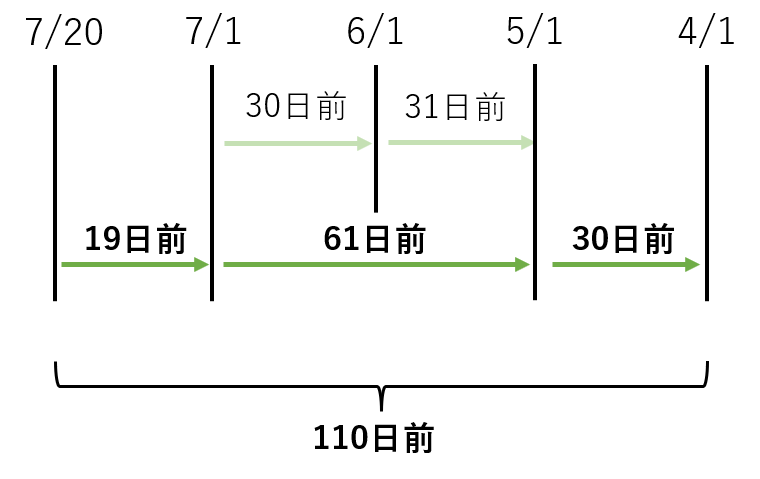
ここまでが2つ目の工程です。
7で割る
この工程では、先ほど求めた「〇日前」という数字を7で割ります。
〇日前を7で割ることで、「〇日前までに1週間が何回繰り返されているか」と「一週間に満たないはんぱな日数が何日あるか」がわかります。
例題の場合
4月1日は基準となる7月20日の110日前であるため
110÷7=15あまり5となります。
この時、「15あまり5」の「15」というのは「15週間」という意味で、「15あまり5」の「あまり5」は、「はんぱな5日間」という意味です。
つまり「15あまり5」は「15週間とはんぱな5日」という意味になります。
表から曜日を求める
最後の工程は、標準的な問題と全く同じです。
7で割ったあまりと同じ数字がふられている列に日付を記入し、曜日を求めます。
例題の場合
4月1日が7月20日の15週間と5日前であることがわかったため
4月1日は5がふられている列に記入すればOKです。
4月1日を記入した列は火曜日の列であるため、4月1日は火曜日だとわかります。
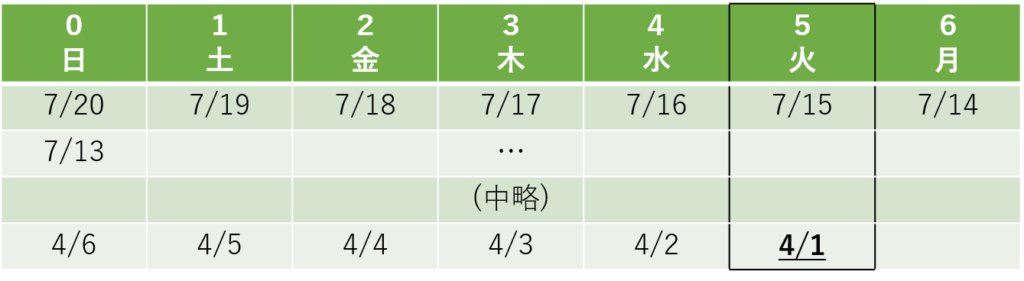
以上が日付をさかのぼるタイプの特殊算の解き方でした。
繰り返しにはなりますが
- 表の曜日と日付はさかのぼって書く
- 何日前かを求める
の2つがポイントになります。
このやり方さえ覚えておけば、迷わずに7で割ったあまりの処理ができるようになります!
ぜひご活用ください!
【番外編】日後と日目
日歴算を解くときに
「基準となる日から曜日を求めたい日が何日後(何日前)であるか」
という考え方をする参考書と
「基準となる日から曜日を求めたい日が何日間か」
という考え方をする参考書があります。
どちらで考えても答えは同じなのですが、1日分曜日がずれると不正解になってしまう日歴算では重要な問題です。
個人的には「何日後」で考えることをおすすめしますが、「何日目」で考えても同じ表を使って考えられます。
表の曜日の上に記入する数字を1から書き始め、7を「7(0)」と記入しておけば問題ありません。
これは標準的な日歴算の問題でも、さかのぼる日歴算でも同じです。
先ほどの例題を活用して解説しましょう。
標準的な日歴算の場合
まず、以下の例題を使って標準的な日歴算の場合を考えてみましょう。
ある年の3月14日が木曜日の時、同じ年の7月2日は何曜日ですか。
この例題の場合、7/2は3/14から数えて111日目にあたります。
※「3/14から7/2までで111日間ある」という意味です。
111÷7=15…6となりますが、この時表を以下のように記入しておきます。

曜日の上の数字を0からではなく、1から記入しておくのが最大のポイントです。
この時、111÷7のあまりである「6」がふられている列に曜日を求めたい日付である7/2を記入すると、7/2が火曜日であるとわかります。
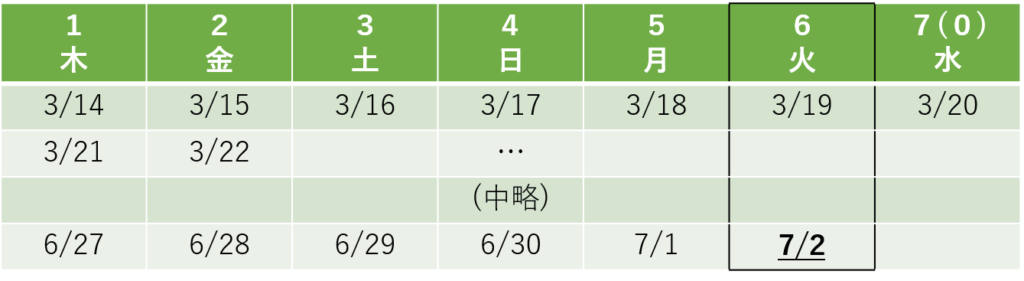
以上が「〇日目」で考えた場合の解法です。
特殊な日歴算の場合
次に、以下の例題を使って特殊な日歴算の場合を考えてみましょう。
ある年の7月20日が日曜日の時、同じ年の4月1日は何曜日ですか。
この例題の場合、7/20を1日目とすると4/1は111日目にあたります。
※「7/20から4/1までで111日間ある」という意味です
111÷7=15…6となりますが、この時表を以下のように記入しておきます。

この時、111÷7のあまりである「6」がふられた列に曜日を求めたい日付である4/1を記入すると、4/1が火曜日であるとわかります。
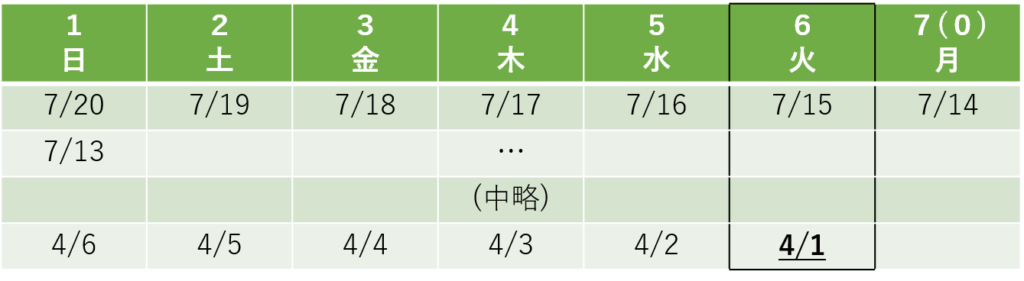
以上が、「何日後(何日前)」か「何日間」かの違いでした。
今回の例題はどちらも7で割ったときにあまりが発生したため、そのあまりの数字がふられている列に日付を記入すれば問題ありませんでした。
ただ、「何日間」で考える場合は、あまりが発生しなかった時に日付を7(0)の列に記入できるかが重要になります。
少しの違いではありますが、正解/不正解を分けうる重要な要素です。
好みもあると思いますので、ご自身に合った解き方を採用してはいかがでしょうか。
まとめ
本記事では、日歴算の前提知識・解き方をご紹介しました。
重要なポイントをまとめます。
- 曜日の周期
- 1か月の日にち
- うるう年
- 表を書く
- 曜日を求めたい日が基準となる日の何日後(何日前)かを求める
- 7で割る
- 表から曜日を求める
- 「〇日後(前)」で考える場合、曜日の上にふる数字は「0,1,2…,6」の順番
- 「〇日目」で考える場合、曜日の上にふる番号は「1,2,3…6,7(0)」の順番
- 日付をさかのぼる問題は曜日と日付をさかのぼって記入していく
以上です!
最後までご覧いただきありがとうございました。
今回ご紹介した知識をご活用いただけると嬉しいです!
検討を祈ります!


