中学受験では絶対に避けては通れない平面図形の面積問題。
出題されない入試はないと言っても過言ではありません。
とはいえ
- 「見たことない図形だと手が止まってしまう」
- 「解き方が全く思いつかない…」
とお悩みのお子さんも多いことでしょう。
そこで本記事では平面図形の面積が苦手な方向けに
面積の問題の全3パターンをご紹介します!
中学受験の面積の問題でこれ以外の解法の問題は出題されません!
これさえ覚えておけば、どんな面積の問題にも対応できます!
ぜひご覧ください!
【前提】面積公式は使えますか?

3つの解法をご紹介する前に、大前提の確認です。
平面図形の面積を求める問題でまず絶対に考えていただきたいのが
「面積の公式で解けないか」ということです。
そもそも中学受験では
- 正方形/長方形
- 三角形
- ひし形 / 平行四辺形
- 台形
- 円 / おうぎ形
など多くの平面図形の面積公式を習います。
ですので、平面図形の面積の問題が出題された際は
「知ってる面積公式で面積を求められる図形か、求められない図形か」を最初に考えましょう。
考える際のポイントは
・面積を求めたい図形の名前は何か
・面積公式は何か
・面積公式で使う辺の長さは全て求められるか
の3つです。
この3点を考えて、「面積公式で解ける!」と判断できれば、あとは公式に当てはめるだけです。
計算ミスに注意して計算しましょう。
【面積公式が使えない】解法はこの3パターン

模試や入試本番では面積公式で計算すればいいだけの単純な問題はほとんど出題されませんありません…。
多くの場合、工夫が必要になります。
しかし、ご安心下さい!!
そういった、面積公式だけでは求められない面積の問題でもこの3つのいずれかで必ず解けます!
その3つの解法とは
- 分割
- 周りから引く
- 移動・変形
です。
詳しく解説します。
【解法①】分割
公式で面積を求められない際は、まず図形を分割して面積を求められないかを検証しましょう。
補助線を引いて、面積を求めたい部分の図形を分割することで、面積公式を使える図形にできないかを考えます。
「分割」を使う例
例えば、このような問題が出題されたとしましょう。
以下の図形の、影がついている部分の面積を求めてください。
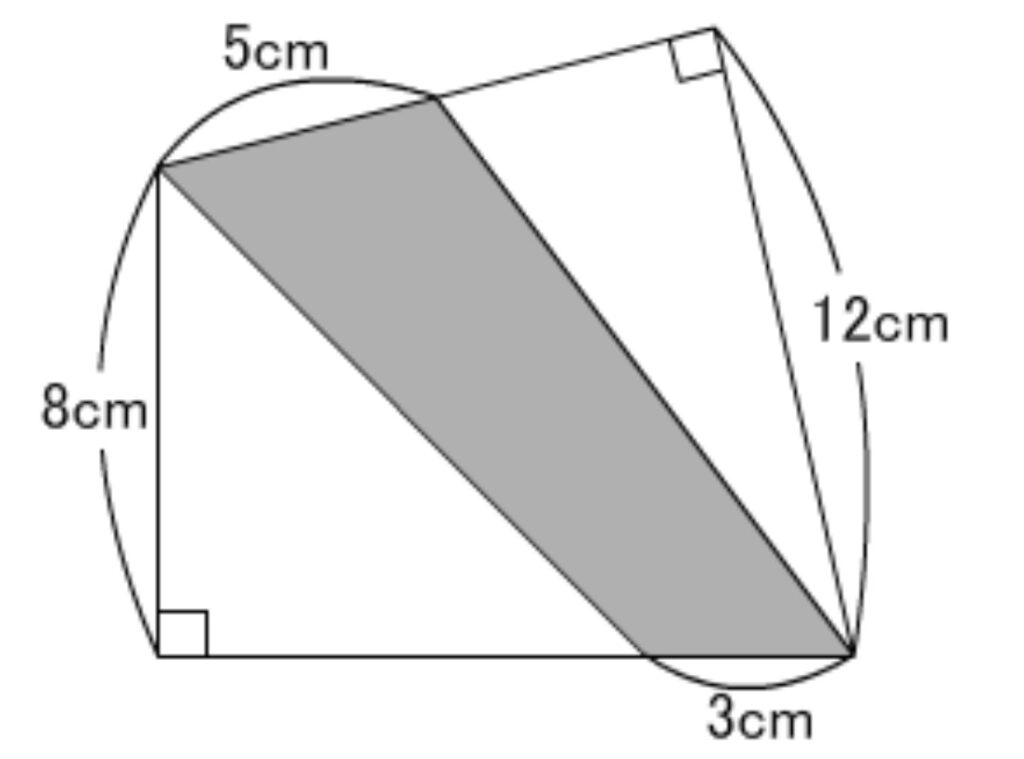
この問題では、面積を求めたい部分の図形は四角形ですが、底辺も高さも分らないため、面積公式は使えません。
そこで、左上の頂点から右下の頂点へ補助線を引いて、2つの三角形に分割します。
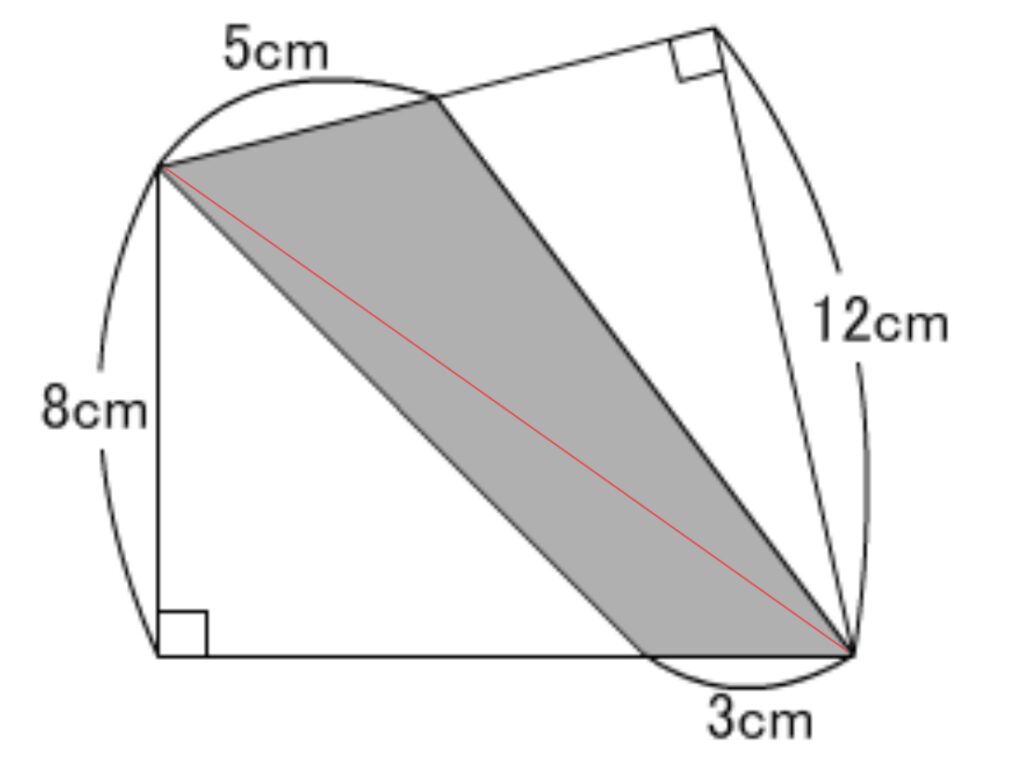
するとどうでしょう。
影がついている2つの三角形はどちらも底辺の長さ・高さがわかるため、面積公式が使える三角形に分けることができました。
これが「分割」です。
なお、分割する際には補助線を引く必要がありますが、補助線の引き方に関してはこちらの記事で解説しておりますので、あわせてご覧ください!
【解法②】全体から引く
分割でも求められそうにない場合は、全体から引いて求められないかを考えましょう。
求めたい部分とその周りも含めた全体の面積から、余分な部分の面積を引くことで、面積を求められないかを考えます。
「全体から引く」を使う例
例えば、このような問題が出題されたとしましょう。
以下の図は、半径6cmの半円を、点Bを中心に45°時計回りに回転させたものです。影がついている部分の面積を求めてください。
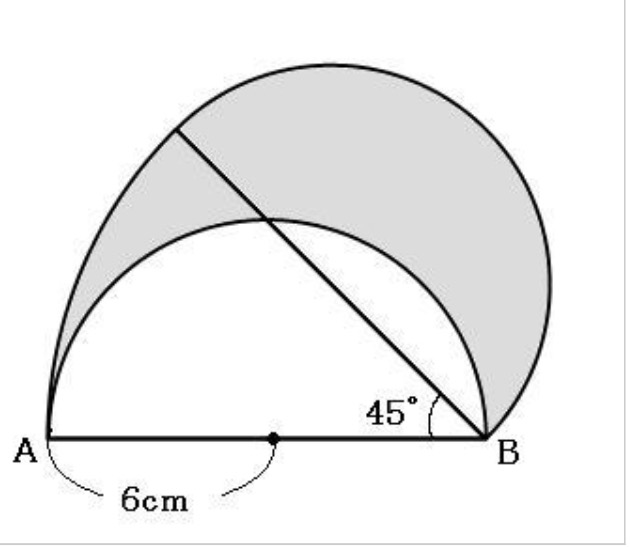
この問題の場合、求めたい図形は明らかに面積公式が使えないうえ、面積公式のある図形には分割できそうにありません。
そこで、全体から白い部分の面積を引くことを考えます。
すると
半径12cm・中心角45°の扇形と半径6cmの半円の面積の和(全体)から半径6cmの半円の面積を引くと、影が付いた部分の面積を求められることに気が付きます。
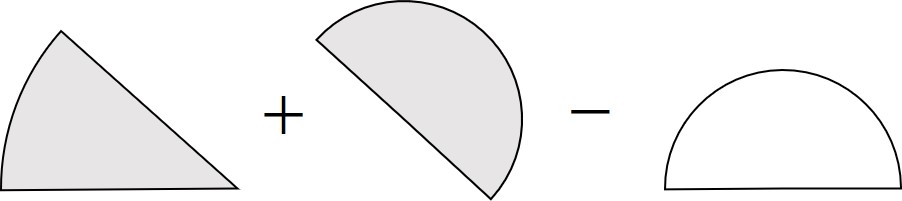
これが「全体から引く」です。
【解法③】移動・変形
分割もしても全体から引いても求められそうにない場合は、「移動・変形」を考えましょう。
面積を求めたい部分の一部もしくは全部を移動 or 変形させることで、面積公式が使える図形にする考えます。
「移動・変形」を使う例題
例えば、このような問題が出題されたとしましょう
以下の図形は、半径10cm・中心角90°の扇形の弧に点D・Fを置き、また半径OB上に点C・Eを置いたものです。斜線部分の面積を求めてください。
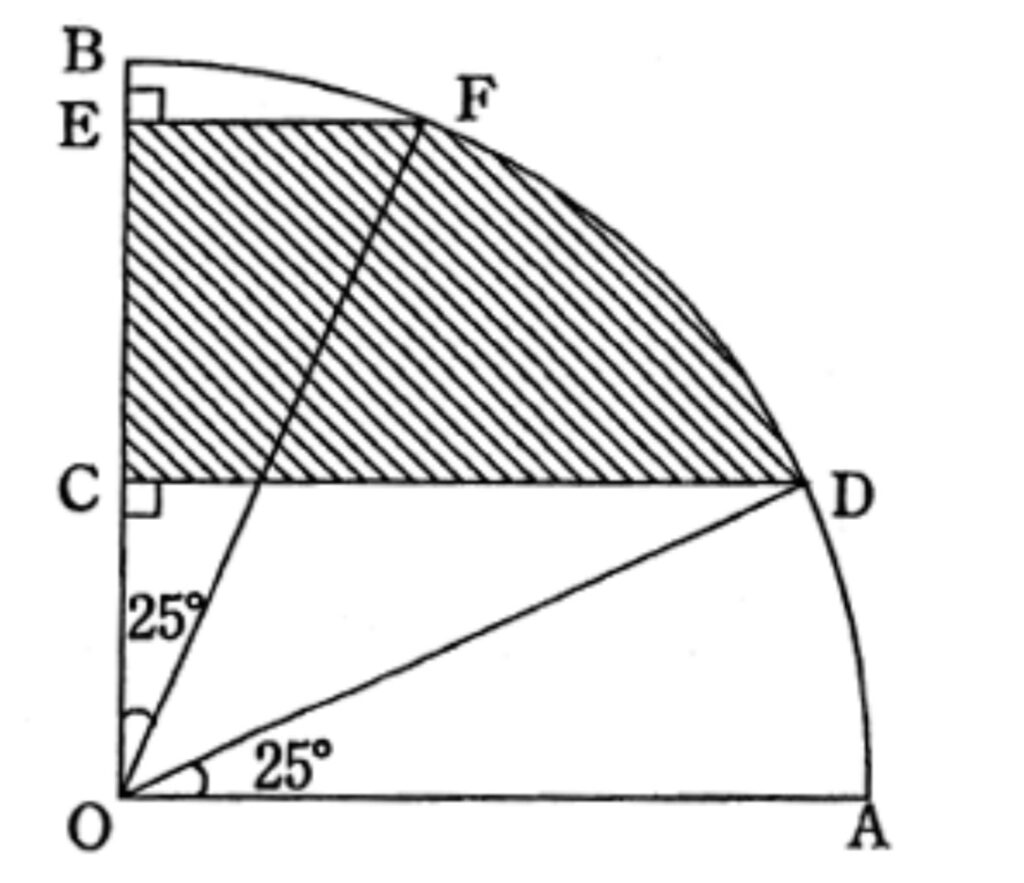
この場合、面積公式が使えないのはももちろん、わかっている長さも扇形の半径しかないため「分割」や「全体から引く」の解法も使えません。
そこで、「移動・変形」を考えます。
まず図形の中の三角形OEFと三角形OCDは面積が等しいことがわかります。(斜辺の長さと三角形の3つの頂点の角度が等しいため、線対称な三角形です。)
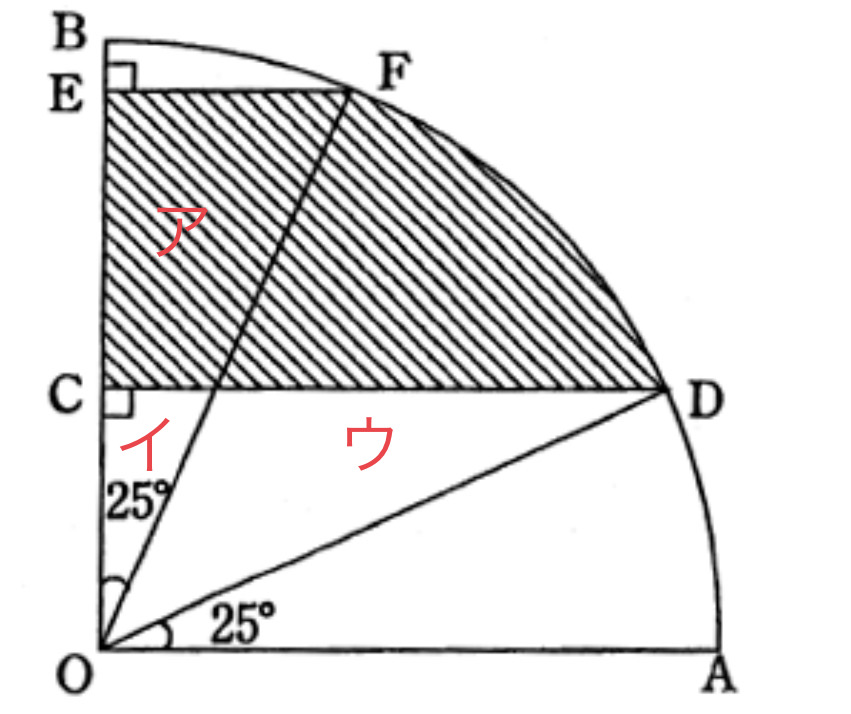
三角形OEFの面積=三角形OCDの面積
(アの面積)+(イの面積)=(イの面積)+(ウの面積)
よって(アの面積)=( ウの面積)といえます。
つまり、面積を求めたい斜線部分の一部である(ア)の部分は(ウ)の位置に移動することができます。
すると、求める斜線部分の面積は、半径10cm・中心角40°の扇形の面積を求めればよいことに気が付くはずです。
これが「移動・変形」です。
なお、「移動・変形」は難易度が高いため、小学校4・5年生ではあまり出番はありません。
まとめ

本記事では、中学受験の面積の問題の全3パターンをご紹介しました。
前提として、まずは
「面積の公式で解けないか」を確認しましょう。
その際のポイントは
- 面積を求めたい図形の名前は何か
- 面積公式は何か
- 面積公式で使う辺の長さは全て求められるか
の3つです。
そして、面積公式で求められない面積は
- 分割
- 周りから引く
- 移動・変形
のいずれかで解きましょう。
中学受験の面積の問題は絶対にこの3パターンで解くことができます。
これさえ知っておけば、初めて見るような面積の問題も取り組みやすくなるはずです。
ですので、ぜひこの3パターンは覚えてしまいましょう。
以上です!ご覧いただきありがとうございました!
皆さんの中学受験がステキな経験になりますように。




